自然のリズムを描いたケルト紋様、書いてみようと思ったら大変だった(;^_^A

「ケルト紋様の幾何学」(アダム・テットロウ著)
ケルトと聞いて想起するのは音楽であり、渦巻き紋様です。渦巻きはよく生命の根源的な象徴的表現とも言われることを度々、本などで目にすることがあります。「ケルト紋様の幾何学」は、その渦巻きをはじめとする始まりと終わりの境界が曖昧なケルト紋様の数々について言及した本です。その本の出だしがおもしろいと思いました。
「古代の人々は、線が持つ力や美しさに魅了された。線が描く模様に、永遠を見出だしたからだ。永遠の本質は数にある。数を学ぶことは、永遠を学ぶことだ。数は永遠である。数は変化しない。数は増減するが、数の性質そのものは不変である。」
まるで蔦が絡み合い始まりも終わりもなさそうなケルトの紋様には、数=幾何学的な要素を見いだすことができる。この本ではそうした紋様の幾何学的な法則性のようなものを解説しています。
私はこうした幾何学なものの法則性などを解説したものは、読んでいて頭が混乱するし苦手なのですが、一見カオス的な紋様がコンパスと定規で作られているということが見えてくるのは、わかっているとはいえ、少しばかり驚きというか、発見なのでした。
あの世界一美しい本と評される「ケルズの書」も、実際細部を見ていくと、そうした幾何学的法則性の上で独特な解釈と装飾を持たせ作られているということがより見えてきて、それが作られるまでの気の遠くなるような作業が想像され、いや、想像さえできないのですが、あらためて驚嘆せざる得ませんでした。
それと、この本にはケルトのベースにあるドルイドの神秘的な考えが、フランク王国メロヴィング朝の国王、異端のカタリ派、シャルトル学派は影響を受けていたと書かれていました。それらがどのような影響を受けていたかがわかりませんが、3つともいろいろな本を読むと倒叙してくる名前なので、ちょっと気になりました。
ケルトの紋様が幾何学的な法則があると書かれていたので、私も方眼紙を購入し、気軽な感じで書いてみたのですが、これが大変でした。これがすぐれた業となると気の遠くなる時間と作業がかかるなと実感(笑)
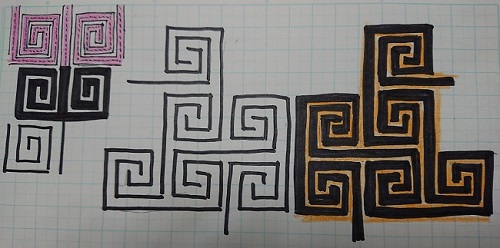
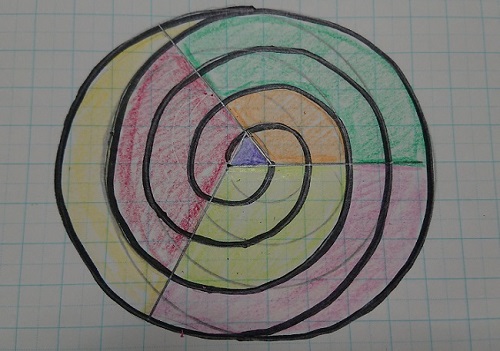

「ケルト、癒しと再生の森」(←クリック)



